I have been trying to write this article for three months now, about how cryptography is actually way more creative than you might think on the surface. The inspiration for this article is an interesting Code kata problem I ran into.

So what's been the delay? Well – the truth is, it took me forever to solve it. While a relatively simple problem on the surface, during the implementation process its complexity revealed itself. Now that I've actually solved it (hurray!) I thought I'd do a quick write up. Warning - my solution was not as elegant as others I've seen submitted. But it got the job done! On the surface this problem seems to consist of just two modules, encoding and decoding.

Encoding – High Level View

You can break this problem into a few steps:

1.     Determine size of the square based on message length

2.     Gain encoding path based on that square size

3.     Generate a square coordinate dictionary based on that square size

4.     Assign the characters of the string to be encoded to a value on the encoding path, then join row by row based on that value's corresponding square coordinates

Step 1 was simple enough - by getting the length of the string we need to encode, squaring it, and using a ceiling function on the result, we can ensure that we get the smallest possible square that will contain all of the characters in the string.

After throwing some code at the wall in my attempt to solve step 2, I realized I might need to break out the handy dandy notebook and draw some squares to see if I could notice a pattern to make the encoding algorithm. It's suprising how pen and paper is often the most important tool for solving a coding problem (or any problem for that matter).

Notice the scribbles, the highlighting, particularly the 7x7 square (which I ended up using as my guinea pig) and then refer to the problem prompt. Why might those areas be significant? The square we generate to encode the string can actually be thought of as a series of squares within one another - I called each of these squares "edges".

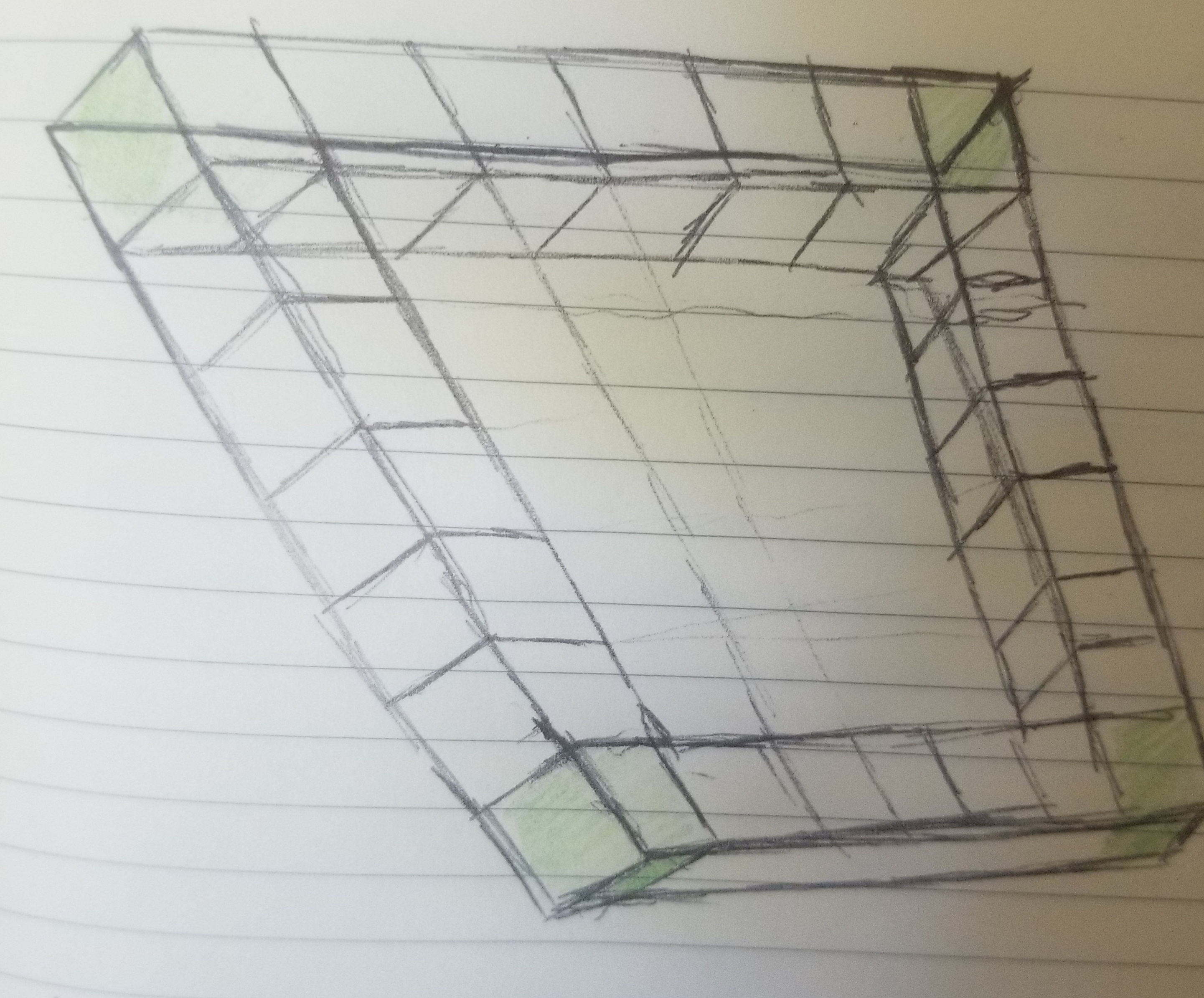
Since we are using four corners of the square at a time as encoding locations, the encoding string can be thought of as a compilation of four number "blocks" ([1,7,13,19] → [2,8,14,20]). These numbers correspond to the position in the squares show above. As we encode the string, these blocks fill the "edge". Notice, there is a set distance between the corners in any one block. This number varies depending on the edge you are on, so we will need to make sure our program recalibrates properly so that it fills the next edge correctly.

Decoding - High Level View

For starters, I like coding in C#. I'm playing with the idea of writing this up in javascript to visualize the process, but can't put the cart before the horse! I have posted my code to the "interlace spiral cypher" repository of my github. Feel free to check it out - still haven't solved it yet, but more to come!

1.     Get the size of the square needed by getting the length of the encrypted string

2.     Use that square size to generate the coordinate dictionary

3.     Simultaneously (a) iterating through the encrypted string in order, selecting characters for placement and (b) iterating through the square coordinate dictionary in order of coordinates, using the correspodning values to determine where I would place the character in our "decoding" array.

While the implimentation of this step didn't take much code, it was tough juggling the various locations in my head. If you're interested in my solution, feel free to head over to my GitHub and check it out. Not sure if I'm going to do anything else with this problem - given how much time I spent on it I'm ready to move on to other things haha.